*** 제가 듣고 보고 경험한 것을 바탕으로 쓰다 보니 다소 주관적일 수 있는 점 양해 바랍니다. ***
*** 제 글들의 내용은 회사나 학교, 시대에 따라 다르거나 변화할 수 있으니 기본 개념이 이렇다는 정도로 이해해주세요. ***

|
1. 콘크리트 물량 산출 |
보의 콘크리트 물량의 산출식은 '(보춤-슬라브 두께)x보폭x보 내폭 길이' 이다. 또는 다르게 표현하면 '(보높이-슬라브 두께)x보두께x보 내폭길이'라고 할 수 있다.

위의 보의 길이가 10m이고 좌우 기둥의 규격(400mm*400mm)을 공제한 내측길이는 9.2m 경우의 물량을 구해보자. 슬라브 두께는 150mm로 가정한다.
콘크리트 물량(m3) = (0.6m-0.15m)*0.4m*9.2m = 1.656m3 이다.
(보통 보 산출시 중심선 기준으로 산출하는 경우가 많은데 그런 경우 10.0m-0.2m-0.2m=9.6m가 내측길이가 된다.)
150mm의 슬라브는 따로 물량을 산출하기 때문에 보의 물량을 산출할때는 이 슬라브 두께를 공제하고 물량을 산출한다. 만약 보 위에 슬라브가 없다면 그땐 슬라브두께의 공제 없이 물량을 산출한다. 보의 길이인 10m가 아니라 내폭길이 9.2m를 적용하는 이유는 기둥 부분은 기둥에서 물량을 산출하기 때문이다.
|
2. 거푸집 물량 산출 |
보의 거푸집은 측면거푸집과 밑면거푸집이 있다.
측면 거푸집 물량(m2) = (보높이-슬라브두께) x 보 내폭길이 *2
밑면 거푸집 물량(m2) = 보두께 x 보 내폭길이
측면 물량의 산식에서 뒤에 2를 곱하는건 보의 측면이 양면이기 때문에 2를 곱한 것이다.
위에 콘크리트 예시로 든 보의 거푸집을 산출해보자.
측면거푸집 물량(m2) = (0.6m-0.15m)*9.2m *2 = 8.28m2
밑면거푸집 물량(m2) = 0.4m*9.2m = 3.68m2
측면 물량 산출 시 슬라브 두께를 공제하는 이유는 보 상부에 슬라브 두께만큼 콘크리트가 타설되어야 하니 거푸집을 굳이 댈 필요가 없기 때문이다. 측면과 밑면 물량 산출시 보 내측길이를 적용하는 이유 역시 좌우 기둥이 타설 된 후에 보를 타설하기때문에 기둥과 중복되는 부분에는 거푸집을 댈 수가 없기 때문이다.


원칙상으로는 위의 그림처럼 보의 측면과 밑면의 물량을 구하는게 맞다. 이렇게 산출하면 슬라브의 밑거푸집을 산출할 때는 보의 밑면의 넓이만큼 중복되는 부분의 물량을 공제해줘야 한다. 이 공제하는 작업이 번거로워서 보통은 아래처럼 슬라브의 밑면거푸집을 쭉 산출하고, 보에서 측면거푸집만 산출하기도 한다. 그럼 보의 밑면거푸집은 슬라브에서 이미 뽑은 셈이니 물량이 빠지거나 중복되지 않는다.

|
3. 보의 정착과 이음 |
보의 철근 물량산출에 앞서 정착과 이음이 어느 경우에 들어가는지 간단히 설명하겠다.
정착은 2가지의 경우에 들어가는데, 보 옆에 보가 없을 경우와 서로 다른 부호의 보가 만날때 정착을 준다. 서로 다른 부호의 보라는 것은 배근이 다르다는 뜻이다. 그래서 정착을 준다.
아래 그림을 보면서 살펴보자.
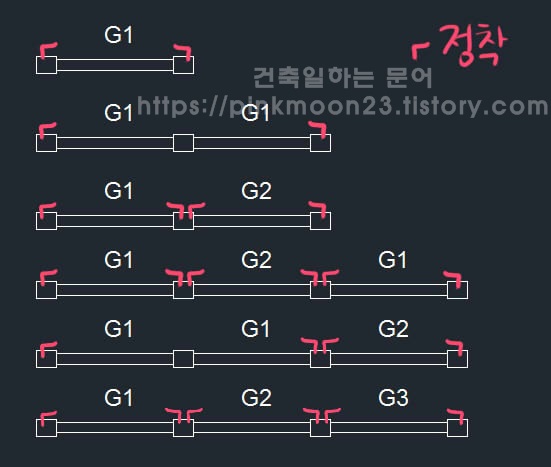
위에 기둥과 기둥 사이에 있는 보의 경우들을 표현한 것이다. 빨간색으로 ㄱ표시는 정착을 표시한 것이다.
1. 보가 1개가 있다. 그럼 좌우에 보가 없는 끝단부이니 좌우에 정착을 준다.
2. 보가 2개가 있는데 G1과 G1이 나란히 있다. 그럼 왼쪽에 있는 G1의 좌측의 단부에 정착 하나, 오른쪽에 있는 G1의 우측의 단부에 정착 하나가 들아간다.
3. 보가 2개가 있는데 G1과 G2가 나란히 있다. 그럼 각각 단부에 정착이 하나씩 들어가고 서로 부호가 다르니 G1의 좌우에 정착 하나씩, G2의 좌우에도 정착 하나씩 들어간다.
4. 보가 3개가 있는데 G1, G2, G1 순서로 보가 있다. 그럼 세개의 보 다 각가 좌우에 다 정착이 들어간다. 만나는 보의 부호가 서로 다르고, 맨앞의 보의 좌측과 맨뒤의 보의 우측은 단부이기 때문이다.
5. 보가 3개가 있는데 G1, G1, G2 순서로 보가 있다. 그럼 우선 맨앞뒤 보의 단부에 정착이 들어가고, 서로 다른 보가 만나는 두번째 보 G1의 우측에 정착, G2의 좌측에 정착 하나가 들어간다.
6. 보가 3개가 있는데 G1, G2, G3 순서로 보가 있다. 그럼 맨앞뒤 단부에 정착이 들어가고 모두 만나는 보가 다르니 각각의 보의 좌우에 정착이 들어간다.
이제는 이음을 설명해보겠다.보를 포함한 수평부재나 수평철근은 보통 8m 간격마다 이음이 들어간다.
만약 보가 하나가 있는데 이게 9m이면 이음이 한번 들어간다.
만약 3m짜리 보 1개와 4m의 보가 나란히 있다면 이는 둘이 합쳐도 8m가 안되기 때문에 이음이 안들어간다.
만약 4m짜리 보 1개와 5m의 보가 나란히 있다면 둘이 합쳐 8m가 넘으니 5m짜리 보에 이음이 한번 들어간다.
만약 7m짜리 보 1개와 10m의 보가 나란히 있다면 둘이 합쳐 17m이다. 8m 간격마다 이음을 한번씩 적용하는것이니 이 경우엔 8m와 16m에 해당하는 10m짜리 보에 이음이 2번 들어간다.
만약 9m짜리 보 2개가 나란히 있다면 둘이 합쳐 18m이다. 또 한개의 보도 이미 8m가 넘으니 각각 이음 한번씩 총 두번이 적용된다.
보의 부호가 서로 다르더라도 보가 계속 이어진다면 8m가 해당되는 지점마다 이음을 준다고 보면 된다.
보의 정착과 이음의 개념은 옹벽의 수평철근의 정착과 이음의 개념과 같다.
그러니 잘 숙지하길 바란다.
|
4. 철근 물량 산출 |
앞의 포스팅에서 보의 배근을 보는 법과 철근을 어떻게 산출하는지 개념을 다루었다. 위에서는 정착과 이음에 대해 배웠으니 이제 보의 철근물량을 산출해보자. 보에서 산출하는 철근은 상부근, 하부근, 늑근, 보조근이다.
상부근(m) = (보길이+(정착길이*정착개소)+(이음길이*이음개소))*상부근개소
하부근(m) = (보길이+(정착길이*정착개소)+(이음길이*이음개소))*하부근개소
늑근(m) = (보길이/늑근간격+1)*((보높이+보폭)*2)
위의 산식은 기본형인 전단형 보의 산식이다.
양단중앙형과 내중외단형의 철근을 구할 땐 위의 산식에서 조금 변형하여 산출하게 된다. 쉽게 말하면 각 구간별로 상부근과 하부근, 늑근을 구한다고 보면 된다. ,
예시로 아래 도면의 보 물량을 산출해보자.

위 도면을 보면 보후보와 보 길이, 기둥 사이즈 등이 표기되어있다. 우선 보의 정착과 이음을 표시하자면 아래도면에 표시한 것과 같다.
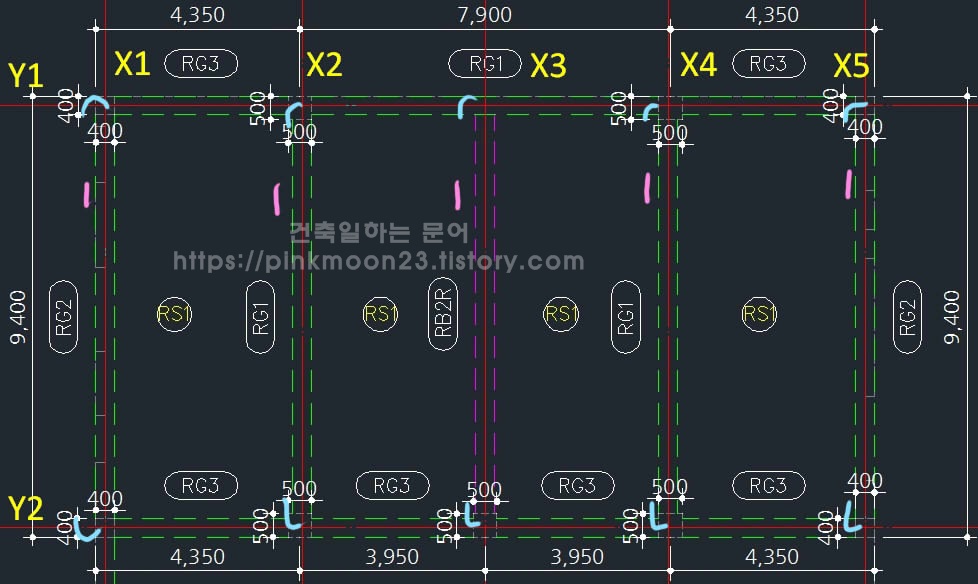

첫번 째 사진은 Y1, Y2열에 있는 보의 정착과 이음을 표시, 두번 째 사진은 X1~X5열에 있는 보의 정착과 이음을 표시한 것이다. (파란선-정착, 분홍선-이음)
각 정착과 이음이 파악이 되었다면 아래 배근들을 참고하여 물량을 산출해보자.
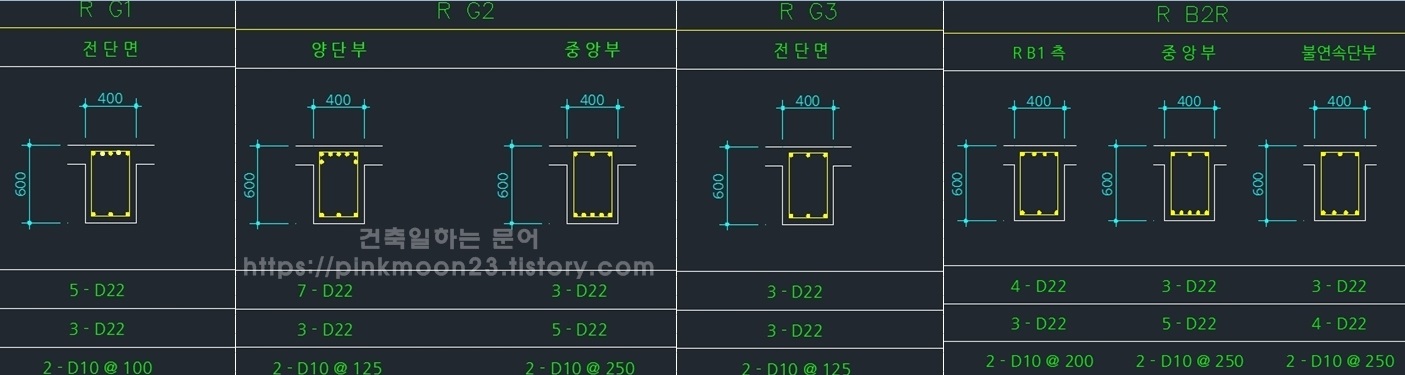
위에서 배운것들과 배근을 토대로 물량 산식을 적어보겠다. 슬라브 두께는 150으로 보겠다. 단위는 콘크리트는 m3(루베), 거푸집은 m2(헤베), 철근은 m이다.
<Y1열 1.RG3>
1. 콘크리트 = ((0.6-0.15)*0.4)*(4.35-0.4-0.25)
2. 거푸집(측면) = (0.6-0.15)*(4.35-0.4-0.25)*2
3. 거푸집(밑면) = 0.4*(4.35-0.4-0.25)
4. 상부근 H22 = (4.35+(정착*2))*3
5. 하부근 H22 = (4.35*(정착*2))*3
6. 늑근 H10 = (4.35/0.125+1)*((0.4+0.6)*2)
<Y1열 2.RG1>
1. 콘크리트 = ((0.6-0.15)*0.4)*(7.9-0.25-0.25)
2. 거푸집(측면) = (0.6-0.15)*(7.9-0.25-0.25)*2
3. 거푸집(밑면) = 0.4*(7.9-0.4-0.25)
4. 상부근 H22 = (7.9+(정착*2)+이음)*5
5. 하부근 H22 = (7.9*(정착*2)+이음)*3
6. 늑근 H10 = (7.9/0.1+1)*((0.4+0.6)*2)
<Y1열 3.RG3>
1. 콘크리트 = ((0.6-0.15)*0.4)*(4.35-0.25-0.4)
2. 거푸집(측면) = (0.6-0.15)*(4.35-0.25-0.4)*2
3. 거푸집(밑면) = 0.4*(4.35-0.25-0.4)
4. 상부근 H22 = (4.35+(정착*2))*3
5. 하부근 H22 = (4.35*(정착*2))*3
6. 늑근 H10 = (4.35/0.125+1)*((0.4+0.6)*2)
<Y2열 1.RG3>
1. 콘크리트 = ((0.6-0.15)*0.4)*(4.35-0.4-0.25)
2. 거푸집(측면) = (0.6-0.15)*(4.35-0.4-0.25)*2
3. 거푸집(밑면) = 0.4*(4.35-0.4-0.25)
4. 상부근 H22 = (4.35+정착)*3
5. 하부근 H22 = (4.35*정착)*3
6. 늑근 H10 = (4.35/0.125+1)*((0.4+0.6)*2)
<Y2열 2.RG3>
1. 콘크리트 = ((0.6-0.15)*0.4)*(3.95-0.25-0.25)
2. 거푸집(측면) = (0.6-0.15)*(3.95-0.25-0.25)*2
3. 거푸집(밑면) = 0.4*(3.95-0.25-0.25)
4. 상부근 H22 = (3.95+이음)*3
5. 하부근 H22 = (3.95*이음)*3
6. 늑근 H10 = (3.95/0.125+1)*((0.4+0.6)*2)
<Y2열 3.RG3>
1. 콘크리트 = ((0.6-0.15)*0.4)*(3.95-0.25-0.25)
2. 거푸집(측면) = (0.6-0.15)*(3.95-0.25-0.25)*2
3. 거푸집(밑면) = 0.4*(3.95-0.25-0.25)
4. 상부근 H22 = 3.95*3
5. 하부근 H22 = 3.95*3
6. 늑근 H10 = (3.95/0.125+1)*((0.4+0.6)*2)
<Y2열 4.RG3>
1. 콘크리트 = ((0.6-0.15)*0.4)*(4.35-0.25-0.4)
2. 거푸집(측면) = (0.6-0.15)*(4.35-0.25-0.4)*2
3. 거푸집(밑면) = 0.4*(4.35-0.25-0.4)
4. 상부근 H22 = (4.35+정착+이음)*3
5. 하부근 H22 = (4.35+정착+이음)*3
6. 늑근 H10 = (4.35/0.125+1)*((0.4+0.6)*2)
여기까지는 전단형이니 위의 식이 어렵진 않을것이다.
<X1열, X5열 RG2>
1. 콘크리트 = ((0.6-0.15)*0.4)*(9.4-0.4-0.4)
2. 거푸집(측면) = (0.6-0.15)*(9.4-0.4-0.4)*2
3. 거푸집(밑면) = 0.4*(9.4-0.4-0.4)
4. 상부근 양단부 H22 = ((9.4/4)+정착)*7*2
5. 상부근 중앙부 H22 = ((9.4/4*2)+이음)*3
→ 양단부와 중앙부 두개의 산식을 하나로 표현하면, (9.4+정착*2+이음)*3 +((9.4/4)+정착)*4*2
6. 하부근 양단부 H22 = ((9.4/4)+정착)*3*2
7. 하부근 중앙부 H22 = (9.4/4*2)*5 +(이음*3)
→ 양단부와 중앙부 두개의 산식을 하나로 표현하면, (9.4+정착*2+이음)*3 +(9.4/4*2)*2*2
8. 늑근 양단부 H10 = ((9.4/4)/0.125+1)*((0.4+0.6)*2)*2
9. 늑근 중앙부 H10 = ((9.4/4*2)/0.25+1)*((0.4+0.6)*2)
기본 식을 이해했다면 위의 RG2 식에서 1,2,5,6번식은 어떻게 나온 것인지 쉽게 파악 가능할 것이다.
그럼 이 양단부와 중앙부의 식을 하나로 합친 식은 어떻게 나온것인지 봐보자.
RG2의 경우 양단부의 상부근은 7개, 중앙부는 3개이다. 이건 다시말하자면 철근 3개는 보 길이만큼 다 가고, 나머지 4개만 양단부에만 간다는 뜻이기도 하다.
그럼 8m 간격마다 들어가는 이음은, 9.4m 길이만큼 가는 철근에는 이음이 적용이 되고, 양단부의 길이는 9.4의 1/4인 2.35m이니 양단부에만 들어가는 철근에는 이음이 들어가지 않는다.
정착은 보의 좌우 끝에 주어지니 양단부에 있는 상부근의 개소만큼 정착이 적용된다.
이 내용을 식으로 표현해보면 '(보길이+정착*2+이음)*보길이만큼 가는 철근개소 +(단부길이+정착)*양단부 구간에만 가는 철근 개소*양단부'로 볼 수 있다. 이 내용은 내중외배근의 경우에도 같다.
<X2열, X4열 RG1>
1. 콘크리트 = ((0.6-0.15)*0.4)*(9.4-0.5-0.5)
2. 거푸집(측면) = (0.6-0.15)*(9.4-0.5-0.5)*2
3. 거푸집(밑면) = 0.4*(9.4-0.5-0.5)
4. 상부근 H22 = (9.4+정착*2+이음)*5
5. 하부근 H22 = (9.4+정착*2+이음)*3
6. 늑근 H10 = (9.4/0.1+1)*((0.4+0.6)*2)
<X3열 RB2R>
1. 콘크리트 = ((0.6-0.15)*0.4)*(9.4-0.4-0.4)
2. 거푸집(측면) = (0.6-0.15)*(9.4-0.4-0.4)*2
3. 거푸집(밑면) = 0.4*(9.4-0.4-0.4)
4. 상부근 좌단부 H22 = ((9.4/4)+정착)*4
5. 상부근 중앙부 H22 = ((9.4/4*2)+이음)*3
6. 상부근 우단부 H22 = ((9.4/4)+정착)*3
→ 산식을 하나로 표현하면, (9.4+정착*2+이음)*3 +((9.4/4)+정착)*(1)
7. 하부근 좌단부 H22 = ((9.4/4)+정착)*3
8. 하부근 중앙부 H22 = (9.4/4*2)*5 +(이음*3))
9. 하부근 우단부 H22 = ((9.4/4)+정착)*4
→ 산식을 하나로 표현하면, (9.4+정착*2+이음)*3 +((9.4/4)+정착)*1 +(9.4/4*2)*2
10. 늑근 좌단부 H10 = ((9.4/4)/0.2+1)*((0.4+0.6)*2)
11. 늑근 중앙부 H10 = ((9.4/4*2)/0.25+1)*((0.4+0.6)*2)
12. 늑근 우단부 H10 = ((9.4/4)/0.25+1)*((0.4+0.6)*2)
외우기보다는 이해를 해야하니 위의 산식들을 눈으로만 보지 말고 배근도를 보면서 직접 적어보면서 참고하길 바란다. 콘크리트와 거푸집 물량을 산출시 보길이가 아닌 좌우 기둥이나 보의 폭을 공제하는 이유는 중복되기 때문에 공제하는 것이다. 그러나 철근은 보 길이만큼 가고 기둥이나 보에 정착을 주기 때문에 좌우부분을 공제하지 않고 보길이만큼 산출하는 것이다.
위의 식에서 늑근의 개소를 산출시 정수로 떨어지게 길이를 바꿔야하고, 늑근 개소에서 '+1'을 하는 경우도 안 하는 경우도 회사마다 지침이 다르니 확인해야 한다.
위의 식에서는 적지 않았지만, 서로 다른보가 나란히 이어서 갈 때 상부근과 하부근에 연장근을 주기도 한다.
Y1열의 경우 RG3, RG1, RG3이 연속으로 이어지는데 상부근과 하부근을 길이만큼 끊어서 배근하면 보가 이어질 수가 없을 것이다. 그래서 보 사이에 있는 기둥만큼 여분의 길이을 주고 철근을 산출하기도 한다.
|
5. 프로그램에서는... |
실제로 물량 산출시 위의 식들을 하나하나 작성하면서 산출하는 것은 아니다. 위의 설명한 내용들을 기본 개념을로 두고 프로그램에서는 단순 수치입력과 체크를 하면 된다.
나의 경우 고려전산의 RC2004와 RC(ver.6.0)을 사용하는데, 보 물량 산출시 프로그램으로 작업하는것은 다음과 같다. 산출에 앞서 보 배근 입력, 정착값과 이음값 설정을 하고, 산출할 때는 산출되는 층, 보부호, 보길이, 좌우단부에 공제되는 길이, 공제되는 슬라브두께, 콘크리트와 거푸집 코드, 보개소, 정착과 이음 체크, 이음 간격 등을 입력하거나 체크하는 작업을 한다. 이렇게 작업을 하고 산출식을 보면 위의 내용들이 쭈욱 나오는 것이다. 이 산식을 이해를 해야 내가 제대로 산출하는지, 해당 공사의 지침서대로 산출하고 있는지를 알 수 있는 것이다.
'건축 > 실무자를 위한 공간' 카테고리의 다른 글
| 골조(구조)물량 산출하기 - 4. 기둥 물량 산출하기 (12) | 2019.07.13 |
|---|---|
| 골조(구조)물량 산출하기 - 3. RC슬라브 물량 산출하기 (17) | 2019.07.03 |
| 철근 단위 중량, 철근 체적(단면적) 정리 (0) | 2019.06.22 |
| 골조(구조)물량 산출하기 - 1. 보의 이해 (GIRDER 거더, BEAM 빔) (21) | 2019.06.15 |
| 골조(구조)물량 산출하기 - 0. 기본 설정, 전반적인 산출 개념 (3) | 2019.06.12 |




댓글